Secondary Greek is a little more complicated. They measure how her one change in the same underlying parameter leads to a change in the primary Greek value, rather than looking at the effect on the option itself.
An important second-order metric is gamma. In fact, it is the only secondary Greek word used regularly by options traders. Gamma measures the percentage change in delta relative to the underlying asset.
Delta is the first derivative of the option price, so gamma is the second derivative.
To understand what this means, we first need to take a step back and define what an option delta is.
Understanding Delta
Option gamma operation
You don’t need to understand the math behind gamma (go on to the next section if you want), but for those interested gamma is more formally defined as the partial derivative of delta with respect to the underlying stock price. will be
The formula is (understanding the normal distribution requires some knowledge of normal distributions):

sauce: http://iotafinance.com
Delta refers to the change in the price of an option with respect to the price of the underlying security. For calls, the delta ranges from 0 to 1.
For puts, the values are -1 and 0. Delta represents how much an option’s price increases or decreases when the underlying moves one point.
Usually, a delta between 0.5 and -0.5 is to be expected when the option is on the money. If the option is far away from the money, the delta value will be close to 0, and if the option is deep into the money, the delta will be close to 1.
This usually means that when the price of the underlying stock rises, the call holders benefit because they get a positive delta. In contrast, the delta value of a put is negative, so put holders believe they will benefit when the underlying stock falls.
It’s important to note that this is not always the case. If another factor is large enough, the data can cancel out.
Delta Impact Calculation
To use the above as an example, imagine the call delta is 0.5. A $1 increase in the underlying stock should increase the call price by approximately $0.50.
If the underlying asset decreases by $1, the price will fall by approximately $0.50. Of course, this assumes that no other pricing variables change.
Now imagine a put delta of -0.5. If the underlying stock rises by $1, the put price will fall by $0.50. However, a $1 drop will increase the price by $0.50.
Option holders will notice that option deltas increase rapidly at certain price points. This is called the explosion delta.
For buyers, this is good news as it can lead to big profits. Of course, the opposite is true for sellers on the other side of the exploding delta.
In fact, delta explosions are the main reason selling unhedged options is so risky.
However, while delta hedging can reduce directional risk due to price movements of the underlying asset, keep in mind that such strategies will reduce alpha as well as gamma. Let’s see why it matters.
What is gamma?
Gamma specifies how much the delta changes when the underlying investment moves by $1 (gamma is in units of 1/$).
In other words, delta indicates how fast the option price changes, while gamma indicates how fast the change occurs.
This means that gamma can be used to predict how delta will behave if the underlying asset changes, thus predicting how the value of the option will change.
Gamma is important because delta is only useful at certain moments.
Gamma gives you an idea of how much an option’s delta changes if the underlying increases or decreases.
Why do we need gamma?
To highlight why gamma is important and how it adds another level of understanding to choices beyond delta, let’s take an example. Imagine two options with the same delta value but different gamma values.
You don’t even need to use numbers in this example. Suffice it to say that one has low gamma and the other has high gamma.
Options with higher gamma are more risky. This is because the impact will be more pronounced if there is an unfavorable movement in the underlying asset.
In other words, if an option has a high gamma value, it is more likely that a volatility swing will occur. Options with a low gamma are preferred as most traders like their options to be predictable.
Another way to describe this is to say that gamma measures how stable option probabilities are.
how gamma changes over time
Since the option delta is dynamic, the gamma should also change constantly. Even the slightest movement in the underlying asset can lead to a change in gamma.
Gamma usually peaks when the stock price is close to the strike price. As we have already seen, the maximum value of delta is 1.
The gamma value approaches 0 as the delta decreases as the option moves in and out of money.
Use gamma to measure changes in delta
Calculating the change in delta using gamma is pretty straightforward. As an example, imagine ABC stock is trading at $47. Suppose delta is 0.3 and gamma is 0.2.
If the price of the underlying stock rises by $1 to $48, the delta will be up to 0.5. Instead, if the stock price drops $1 to $46, the delta drops to 0.1.
Long and short options with gamma
For long option holders, gamma means that profits accelerate for every dollar the underlying moves in your favor. Those are long gammas.
This is because gamma increases an option’s delta as it approaches or goes deeper into the money.
Therefore, every $1 increase in the underlying asset means a more efficient return on capital.
This same concept means that losses slow down when the underlying moves $1 against the holder’s favor.
Conversely, gamma poses risk to option sellers. Because if there are winners in the equation, there must also be losers. Just as gamma accelerates long option holders’ gains, it accelerates sellers’ losses.
Similarly, slower losses for holders lead to slower directional gains for sellers.
The Importance of Correct Prediction
Making accurate forecasts is essential, even when buying or selling. As a buyer, a high gamma value and an incorrect forecast could mean that the option moves into the money and the delta moves towards 1 sooner than expected.
This means that the delta will drop faster than expected.
Inaccurate forecasts are equally problematic if you are a seller. A high gamma can mean that positions are going downhill at an accelerating rate as sold options move into money. However, if the forecast is accurate, a higher gamma can lead to faster losses for sold options, with positive results.
Effects of Volatility on Gamma
Money options have a higher gamma when volatility is low. This is because volatility decreases when the time value of options is low. Then, as the underlying stock approaches the strike price, you will see a dramatic rise.
However, when volatility is high, gamma is typically stable across strike prices. The reason is that the time value tends to be greater when options are deeply tied to the money or out of hours.
The value of time changes less dramatically as the options get closer to the fund. This keeps gamma low and stable.
Expiration risk
Another aspect to consider is expiration risk. The closer the option expires, the narrower the probability curve.
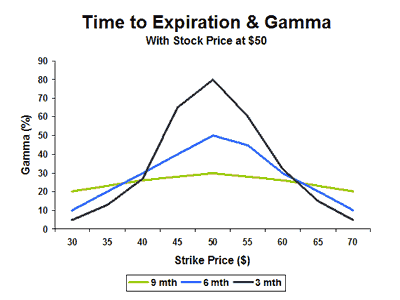
Lack of time for the underlyings to go far out-of-the-money strikes reduces the probability of them going in-the-money. The result is a narrower delta distribution and a more aggressive gamma.
The safest way to use your understanding of gamma to your advantage is to roll and close your position at least 7 (and sometimes 10) days before expiration.
If you wait longer than 7 days, you are more likely to see dramatic shifts from losing trades to winning trades and vice versa. Buyers may benefit from this trend, but it is especially risky for sellers.
List of gamma positive strategies
List of gamma-negative strategies
-
short call
-
short put
-
short straddle
-
short strangle
-
vertical credit spread
-
covered call writing
-
covered put light
-
iron condor
-
butterfly
-
long calendar spread
summary
-
Gamma measures the percentage change in delta relative to the price of the underlying asset.
-
All long options have positive gamma and all short options have negative gamma.
-
A position’s gamma indicates how much a $1.00 change in the underlying changes the option’s delta.
-
To avoid increasing gamma risk, we do not hold trades until expiry.
About the Author: Chris Young has a degree in Mathematics and 18 years of experience in finance. Chris is British, but he has worked in the US and most recently in Australia. His interest in options was first sparked by the “Trading Options” section of the Financial Times of London. He was determined to pass this knowledge on to a wider audience and in 2012 founded Epsilon He Option.
Related article

