However, it’s still worth knowing what rho means, as it provides another dimension to understanding how an option’s price can fluctuate.
What is a row?
Rho measures how sensitive an option’s value is to changes in the risk-free interest rate. The reason this is the least important indicator for Greece is that risk-free interest rates rarely exhibit significant or unexpected changes.
Moreover, even if interest rates fluctuate, the impact on option prices is minimal. This means that Rho has more long-term effects (much like Vega) and minimal impact on short-term options.
Note that rho can also be used to book multiple option positions. In this case rho refers to the total risk of the exposure to changes in interest rates.
The amount that represents how much an option’s value would change if the risk-free interest rate changed by 1 percentage point, whether the rho is used in the book of a single option or multiple option positions.
Option Rho Mathematics
You don’t need to understand the math behind Rho (skip to the next section if you want). However, for those interested, rho is more formally defined as the partial derivative of the option price with respect to the (risk-free) interest rate.
The call option rho formula is (understanding it requires some knowledge of the normal distribution): A similar formula exists for put options.

sauce: iota finance
Calculation of Rho influence
To understand the above, assume the option value is $3.25, the Rho is 0.5, and the risk-free interest rate is 1.5%. In theory, this means that for every 1% increase in interest rates, the price of the option increases by $0.50. So if interest rates rise from 1.5% to 3.5%, the theoretical rate of increase would be:
$3.25 + 0.5 x 2 = $4.25
If interest rates drop by 2%, you’ll see a drop instead.
$3.25 – 0.5 x 2 = $2.25
If the option’s low is negative of -0.5, the opposite happens — the value goes down as interest rates go up:
$3.25 + -0.5 x 2 = $2.25
But when interest rates go down, the value goes up.
$3.25 – -0.5 x 2 = $4.25
Why do interest rates affect options?
It’s easy to see why the factors that lead to other Greek sensitivities affect option value. For rho it is less obvious. Interest rates are, after all, interest rates on bonds, whereas stock options are stocks with no fixed rate.
To understand why interest rates affect options, it is important to first clarify what we mean by risk-free interest rates.
What is a risk-free interest rate?
In asset management, some types of investments are considered risk-free. For example, US government bonds are backed by a government agency and are therefore risk-free. There is little risk of default for depositors as the government is unlikely to suffer serious financial problems.
In other words, if you buy government bonds, the risk of losing your investment is minimized. The risk-free interest rate is the lowest rate you can earn when there is zero risk on the money you borrow.
Optional Carry Cost
The main reason rho is important is the cost of carry. Traders often borrow money to buy financial instruments, which incurs maintenance costs to hold options. Additionally, even if traders have money they don’t need to borrow, there are maintenance costs. Traders can instead invest this same amount in an interest-earning account.
As a result, buying a call is cheaper than buying the underlying asset, but the cost of carry is included in the price of the call. Therefore, the cost of the call scales with the risk-free rate.
call and put low
If rho is positive, its value increases as interest rates rise and decreases as interest rates fall (at least in theory). This assumes that all other elements remain the same as when using any other Greek word.
Rho is positive for long options (long calls and short puts) but negative for short options (short calls and long puts). In other words, while rising interest rates are generally good news for long options, short options tend to profit if interest rates fall.
To understand why, let’s use an example. Suppose ABC stock is trading at $35. It would cost him $3,500 to buy 100 shares, but instead he could buy the next month’s at-the-money call for $3.50. So for just $350, you get the same rewards as if you bought the stock, but with less risk. What’s more, he can hedge his investment by investing the rest of his $3,150 in Treasury bonds. If interest rates are found to rise, the price of the call will also rise, making it a good investment.
In addition, traders are more likely to buy calls when interest rates are high because they save more by buying options than by buying the underlying stock. This increased demand can also push up option prices.
Conversely, if current interest rates are low, you may decide to stop buying options and buy the underlying stock instead. This is because if you keep your money with a brokerage firm, you will earn very little interest. Thousands of other investors think exactly the same, which is why more people buy stocks than call options. As a result, the price of the call option will decrease.
Instead, consider how interest rates affect long puts. To play the underlying asset down, short the stock or go long the put option. The first option means generating cash with interest. The second option is less expensive, but you can’t add interest to the brokerage and add cash. As a result, the first option is more attractive when interest rates are high, showing why long put options are devalued when interest rates are high.
Does Volatility Affect Rho?
Volatility is a major factor for most Greeks, but it only indirectly affects the low via delta. How volatility affects low depends on whether the option is out-of-the-money, at-the-money, or in-the-money.
out of the money
If the option is out-of-the-money, it has a strike price above (for calls) or below (for puts) the market price of the underlying asset. Rho is especially worthless against deep out of money options. Increased volatility yields value because the delta is higher and the low is higher.
at the money
An option-at-the-money strike price is approximately (if not exactly) the current market price of the underlying stock. Virtually immune to volatility. Delta remains flat as it increases. That is, there is no change in the row. However, watching the low is useful for at-the-money options as it can provide an indication of the future price trend of the underlying asset. If an option attracts investors’ attention, it is more likely to be profitable.
in the money
An in-the-money call option has a strike price below the market price and a put option has a strike price above the market price. An increase in volatility means a decrease in delta, which leads to a decrease in low.
how to use rho
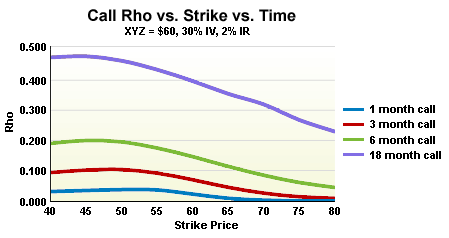
You can expect the low to be high when the option is in the money and low when the option is out out. Options with longer time to maturity also have a higher Rho. This is very different from other Greeks.
If interest rates change unexpectedly, Rho has a bigger impact. This is because sudden rate changes generally increase market volatility and increase option prices.
Still, it’s only worth watching the low if the option has a long time to expiration. This applies to both calls and puts. This is because the extrinsic value is low, so interest rates have minimal impact on the premium as the option nears maturity. For example, lows can affect Long Term Equity Expected Securities (LEAPs) because their maturity dates are usually at least two years.
Rho is the least used of all the major Greek metrics, but it’s still worth knowing what it means and how it works. You can then decide whether to focus on this metric or her other four. If you’re using LEAP, you’ll notice that rho has some effect. However, when trading short-term options, you are unlikely to notice the low making a big difference.
About the Author: Chris Young has a degree in Mathematics and 18 years of experience in finance. Chris is from the UK, but he has worked in the US and most recently in Australia. His interest in options was first aroused by the “Trading Options” section of the Financial Times (London). He was determined to spread this knowledge to more people and in 2012 he founded Epsilon Options.
Related article:

