To Chanika Takar and Rekit Pachanekar
In my last blog, I explained the basics of options trading. In this blog, we go a step further and discuss strategies regarding options trading. There are many options trading strategies that you can find, but only a few are called the most popular strategies among option traders.
Find out all of this in this blog that covers:
List of options trading strategies
Below is a list of options trading strategies you can learn.
And there is so much more you can explore!
Most Popular Options Trading Strategies
There are quite a few options trading strategies available in today’s trading environment. The most popular options trading strategies are:
- spreads and butterflies
- put-call parity
spreads and butterflies
Spreads, or rather spread trading, buys and sells the same option class at the same time, but with different expiration times and strike prices. Spread option trading is used to limit the risk, but on the other hand it also limits the reward for those who indulge in spread trading.
Therefore, if we are only interested in buying and selling call options on a security, we call it a call spread, and if we are only interested in puts, we call it a put spread.
Depending on the changing factors, spreads can be classified as follows:
- Horizontal Spread – Different Expiry Dates, Same Strike Price
- Vertical spreads – same expiration date, different strike prices
- Diagonal spread – different expiry, different strike price
Note that the option value is based on the underlying security (in this case, the stock price). Therefore, option spreads can also distinguish between when prices are expected to rise (bull spreads) and when prices are expected to fall (bear spreads).
bull call spread
With bull call spreads, you buy multiple options to offset potential losses if the trade doesn’t go your way.
Let’s try to understand this using an example.
Below is a table of options available at different strike prices with the same underlying stock and the same expiration date.

Generally, if you do your analysis and expect the stock to rise to $200, one way is to buy a call stock option with a $15 premium and a $180 strike price. So if we are right and the stock closes at $200 at expiry, we bought it at a strike price of $180 and paid a premium of $15 so ($20 – $15) = $5 profit. put it in your pocket.
But if we were wrong and the stock closed below $180, we would not exercise the option and would lose $15 of premium. One workaround is to buy a call option with a price of $15 and a strike price of $180, and sell a call option with a call option price of $10 for $200.
So, if the stock’s price closes at $200 at expiry, you can exercise your purchased call option with a profit of $5 (see above). Also, since the owner does not exercise the call option, he can profit from the $10 premium he got from selling the call option. So with this method, the total profit is ($5 + $10) = $15.
If the stock price rises above $200 and the holder exercises the put option, the increase in profit from the call option bought at $180 will be the same as the loss accumulated from the call option sold at $200, so the profit will always be $15 on maturity, even if the stock price exceeds $200.
Let’s create a table to understand different scenarios.

You will also understand how to implement the bull call spread, how to implement it using Python and how to check the bull call spread payoff diagram.
bare put spread
The bull call spread was executed when the stock price was expected to rise, but what if the analysis reveals that the stock price is going to fall? In that case, please use the double-page spread with bears.
Let’s assume we’re looking at different strike prices for puts on the same stock with the same maturity date.
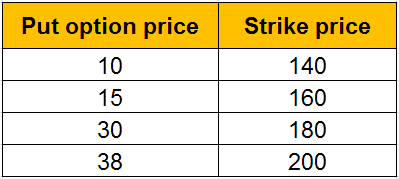
One way is to buy a put option with a strike of $160 at a premium of $15 and sell a put option with a strike of $140 at a strike of $10.
So create a scenario table like this:
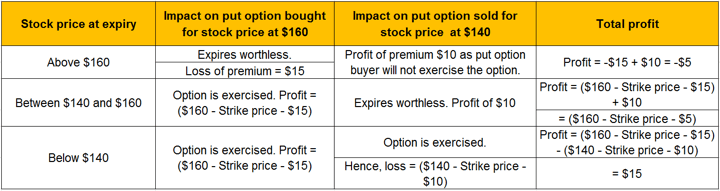
In this way, you can minimize your losses by buying and selling options at the same time.
butterfly spread
A butterfly spread is actually a combination of a bull spread and a bear spread. An example of a butterfly option strategy consists of a body (middle double option position) and wings (two opposite end positions).
Considering that we have seen detailed scenarios on the basics of options trading, why not combine some options?
Understand the key concepts that many professionals use in options trading. This is called Put-call parity. Let’s explore this concept of put-call parity in Python.
put-call parity
Put-call parity is a concept that anyone interested in trading options should understand. By understanding put-call parity, we can understand how the values of call options, put options, and underlying assets relate to each other. This allows you to create other synthetic positions using different options and stock combinations.
Put-call parity principle
The put-call parity principle defines the relationship between the prices of European put options and European call options. Both have the same underlying asset, strike price and maturity date. Any deviation from put-call parity creates an arbitrage opportunity. Traders can use this opportunity to make risk-free profits until put-call parity is re-established.
The put-call parity principle can be used to validate options pricing models. Such a model can be considered incorrect if the option price calculated by the model violates the put-call parity rule.
About put-call parity
To understand put-call parity, consider a portfolio ‘A’ consisting of call options and zero-coupon bonds. The amount of zero-coupon bonds you hold equals the call strike price. Consider another portfolio ‘B’ containing a put option and an underlying asset.
S0 is the initial price of the underlying asset and ST is the price at expiration.
Let ‘r’ be the risk-free rate and ‘T’ be the expiration date.
At time ‘T’, given the risk-free rate ‘r’, the zero-coupon bond is worth K (the strike price).
Portfolio A = Call Option + Zero Coupon Bond
Portfolio B = Put Option + Underlying Asset
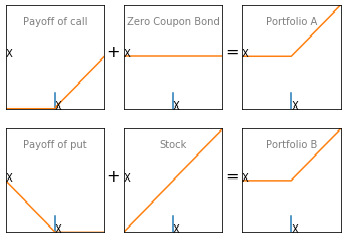
In the image above, if the stock price is higher than X, the call option will be exercised. Otherwise, zero coupon bonds are held. Therefore, at ‘T’, the value of portfolio A is given by max(ST, X).
If the stock price is lower than X, the put option will be exercised. Otherwise, the underlying asset is retained. Therefore, at ‘T’, the value of portfolio B is given by max (ST, X).
If two portfolios are equal at time ‘T’, they should always be equal. This gives us the put-call parity equation.
Formula for put-call parity:
C + Xe-rT = P + S0
In this formula,
- C is the European call option premium.
- P is the European put option premium.
- S0 is the spot price of the underlying stock.
- And Xe-rT is the present value (discount value) of the zero-coupon bond (X).
Put-call parity requirements
To preserve put-call parity, the following conditions must be met: However, in the real world, they rarely apply, and some changes to the put-call parity formula may be required accordingly. This blog assumes that these conditions are met.
- The underlying shares do not pay dividends over the life of the European option
- No transaction costs
- no tax
- Shorting is allowed and there is no borrowing fee
Put-call parity is therefore held in a frictionless market where the underlying stock does not pay dividends.
Arbitrage opportunity
In options trading, violating the put-call parity principle encourages traders to take advantage of arbitrage opportunities.Ann arbitrage trader Go long an undervalued portfolio and short an overvalued portfolio for a risk-free profit.
How to take advantage of arbitrage opportunities?
To illustrate how trading can take advantage of arbitrage opportunities, let’s consider a few example numbers. Assume a stock spot price of $31, a risk-free interest rate of 10% per annum, three-month European call and put premiums of $3 and $2.25 respectively, and a strike price of $30.
In this case, the value of Portfolio A is
C+Xe-rT = 3+30e-0.1 * 3/12 = $32.26
The value of Portfolio B is
P + S0 = 2.25 + 31 = $33.25
Portfolio B is overvalued, so the arbitrageur can profit by going long Portfolio A and short Portfolio B. You can get arbitrage profit by following these steps:
- Short the stock. This will result in a cash inflow of $31.
- Sell put options. This will result in a cash inflow of $2.25.
- Purchase call option. This will generate a cash outflow of $3.
- The total cash inflow is -3 + 2.25 + 31 = $30.25.
- You invest $30.25 in a 3-month zero-coupon bond with an annual interest rate of 10%.
- The return from the zero coupon bond after 3 months is 30.25e 0.1 * 3/12 = $31.02.
If the share price at expiration is above $30, the call option will be exercised, and if the share price is below $30, the put option will be exercised. In both scenarios, the arbitrageur buys his 1 share for $30. This stock is used to hedge shorts.
Total profit from arbitrage = $31.02 – $30 = $1.02
Let’s look at some code.
Python code for plotting the graph
The code below can be used to plot the portfolio payoff.
Conclusion
Option trading strategies such as butterfly, spread and put call parity are among the most widely and commonly used. You can trade options in the best possible way by applying options trading strategies according to your requirements.
If you want to learn more about options trading, you can enroll in the following courses. Systematic options tradingThis course will help you create options strategies, backtest, implement, live trade, and analyze performance. Also, in this course, you will learn how to narrow down your options and find profit potential, expected profit, and strategy payoffs. Additionally, in this course you will learn options trading strategies such as butterfly, iron condor and spread strategy.
Disclaimer: All data and information provided in this article are for informational purposes only. QuantInsti® makes no representations as to the accuracy, completeness, currency, suitability or validity of the information in this article, nor any errors, omissions or delays in this information or any loss resulting from its presentation or display; We are not responsible for injury or damage. use. All information is provided as-is.

