Volatility is an important factor for traders to consider as volatility can have a significant impact on investment returns. Volatile stocks and markets can be dealt with by taking measures to adjust risk.
This post explains how to calculate historical volatility in Python and various ways to measure risk-adjusted returns based on it.
Contents of this blog:
What does volatility mean?
The up and down movement of a security over a period of time is called volatility. Volatility is one of the factors that define security risk. In general, the higher the volatility, the higher the security risk. A security is considered volatile if its price changes slowly over a longer period of time.
Conversely, if the price of a security fluctuates rapidly over a short period of time, its price is considered more volatile. Volatility is best measured by calculating the standard deviation of annualized returns over a period of time.
Volatility measures the dispersion of returns for a particular security.it plays an important role option trading.
The two main volatilities are:
- implied volatility and
- historical volatility.
Implied Volatility
First, let’s talk about implied volatility. Implied volatility is the expected future volatility of a stock. Implied volatility shows the potential movement of a stock price but does not predict the direction of movement. High implied volatility means that the market is pricing in the potential for a stock to move significantly in either direction.
If the implied volatility is low, the price may not move much or make unpredictable changes.
Implied volatility is one of the key determinants in pricing. optionAs the implied volatility increases, the value of the option increases. This is because higher implied volatility suggests greater potential volatility in stock prices.
Implied volatility is Black Shoals Enter all the parameters required to solve for option prices via the Black-Scholes model, get the actual market price of the option, and calculate the formula by undoing the implied volatility parameter To do.
historical volatility
Historical volatility is discussed here because historical data is the best way to judge a strategy’s performance based on historical data.
Historical volatility is derived from time series of historical price data, while implied volatility is derived using market prices for traded derivative instruments such as option contracts.
Let’s look at an example of calculating the historical volatility of NIFTY’s risk-adjusted returns.
First, use NumPy’s log function to calculate the logarithmic return using the NIFTY closing price. We then use Pandas’ rolling_std function and NumPy’s square root function to calculate the annualized volatility.
The rolling function uses a window of 252 trading days. Each day in the selected lookback period is weighted equally. Users can choose longer or shorter durations as per their requirement.
output:
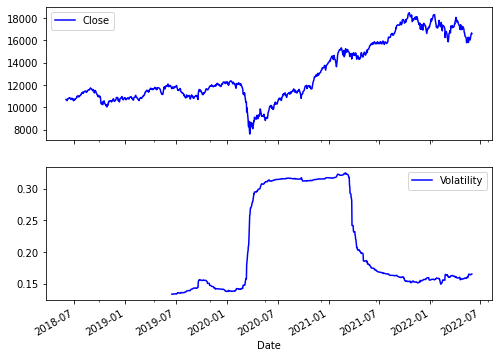
The above output shows that volatility was highest between July 2020 and June 2021.
What is risk-adjusted return in trading?
A risk-adjusted return is a calculation of the return (or potential return) for trading a financial instrument such as a stock. Risk-adjusted returns are often expressed as ratios.
Purpose of the risk adjustment
Risk-adjusted returns are a key component of successful long-term investing and are often overlooked or misunderstood by traders unfamiliar with the area. Risk-adjusted returns are perhaps the most important and least understood part of investing.
Before making any investment decision, we advise you to weigh the potential return and risk of any investment so that you have a full understanding of the risk/return ratio.
Risk-adjusted rate of return in Python
Now let’s find different measures along with their respective formulas for risk-adjusted returns in Python. The countermeasures are as follows.
- sharpe ratio
- information ratio
- Modigliani ratio (M2 ratio)
- trainer ratio
- jensen’s alpha
- coefficient of determination
- Sortino ratio
sharpe ratio
Introduced by Nobel laureate William F. Sharp in 1966, the Sharpe ratio is a metric for calculating risk-adjusted returns. The Sharpe ratio is the average return obtained over the risk-free rate per unit of volatility.
The Sharpe ratio formula is:
$$Sharpe \ ratio = \frac{(Mean \ return − Risk \ free \ rate)}{standard\deviation of \ return\}$$
Below is the code to calculate the Sharpe ratio in Python.
Information ratio (IR)
The Information Ratio is an extension of the Sharpe Ratio that adds the return of the benchmark portfolio to the input. Measures a trader’s ability to generate excess returns compared to a benchmark.
The formula for calculating the information ratio is:
$$Information \ ratio = \frac{(Portfolio \ return − Benchmark \ rate \ of \ return)}{Tracking \ error}$$
The “tracking error” in the above formula is the standard deviation of excess return over the benchmark return.
Below is the code to calculate the Information ratio in Python.
Modigliani ratio (M2 ratio)
The Modigliani ratio measures the return of a portfolio adjusted for the risk of the portfolio relative to the risk of the benchmark.
To calculate the M2 ratio, first calculate the Sharpe ratio and multiply it by the annualized standard deviation of your chosen benchmark. Then add the risk-free rate to the derived value to get the M2 ratio.
The Modigliani ratio is
$$Modigliani \ ratio = SR * \ benchmark standard \ deviation \ + (rf)$$
Below is the code to calculate the Modigliani ratio in Python.
trainer ratio
The Treynor ratio was developed by American economist Jack Treynor, one of the inventors of the Capital Asset Pricing Model (CAPM).
The Treynor ratio is a risk/return measure that allows traders to adjust portfolio returns to systemic risk. A higher Treynor ratio result indicates a portfolio with higher return potential.
The formula for the Trainor ratio is:
$$Treynor \ ratio = \frac{Portfolio \ return – Risk \ free \ rate}{\\Portfolio Beta\}$$
Below is the Python code for the Treynor ratio.
jensen’s alpha
Jensen’s alpha is a risk-adjusted performance measure that represents the average return of a portfolio or investment above or below that predicted by the Capital Asset Pricing Model (CAPM).
A portfolio or investment’s beta and average market return are given.
Jensen’s alpha formula is:
$$alpha = R(i) – (R(f) + B x (R(m) – R(f)))$$
Where,
R(i) = portfolio or investment realized return
R(m) = realized return of the appropriate market index
R(f) = risk-free rate
B = Beta of the investment portfolio with respect to the selected market index
In Python, Jensen’s alpha is calculated as follows:
coefficient of determination
R-squared is the proportion of predictable variation in the dependent variable from the independent variables.
It is a statistical ratio whose primary purpose is to predict future outcomes or test hypotheses based on relevant information. It provides a measure of how well a well-observed outcome is reproduced by the model based on the proportion of total variation in the outcome explained by the model.
The formula for R-squared is:
$$R^2 = 1 – \frac {Unexplained \ Variation}{Total \ Variation}$$
Let’s see how to calculate R-squared using Python. Here is the same code:
Sortino ratio
The Sortino ratio is sharpe ratioHowever, the Sharpe ratio includes both upward and downward volatility, while the Sortino ratio represents only downward volatility.
Similar to the Sharpe ratio, the higher the Sortino ratio, the higher the return per unit risk.
Since most investors are only concerned with downside volatility, the Sortino ratio represents a more realistic picture of downside risk.
Whether you use the Sortino or Sharpe ratio to value an investment, whether analyzing total volatility or downside volatility, is based solely on the individual. Both are commonly used for different applications.
The Sortino ratio is given by
$$Sortino \ ratio = \frac{(Expected \ return – Risk \ free \ rate)}{\minus \standard\deviation of asset\return\}$$
Let’s see how to calculate the Sortino ratio in Python. Here is the python code for the same:
So this is how we calculated historical volatility in Python, on which we also based various measures of risk-adjusted returns.
Learn how to optimize your portfolio in Python using Monte Carlo simulations.
Advantages of using risk-adjusted return ratios
Now let’s look at the benefits of using indicators aimed at risk-adjusted returns. Measuring risk-adjusted returns can help you:
- Portfolios consisting of different financial instruments can be evaluated. Each bears a risk according to its position in the market.
For example, the stock price may crash due to a scenario such as a management change, while other stocks in the portfolio may fluctuate according to the market.
- Measuring risk-adjusted returns helps make more accurate comparisons between risky assets.
- One of the reasons losses occur is poor risk management.
Therefore, understanding the risk and return trade-offs using the above tools will help traders plan their portfolios and make smarter financial decisions.
Disadvantages of using risk-adjusted return ratios
The disadvantages of using instruments aimed at risk-adjusted returns should be known to traders who are aware of the negative consequences of failing to pay attention to the following factors:
- Calculating investment returns often requires looking at past performance. This can be misleading without considering the effects of inflation and other factors over time.
- Market prices for financial instruments mean that risk-adjusted return results become obsolete as soon as market prices fluctuate.
- Risk-adjusted returns do not reveal expected future returns.
Conclusion
A measure of risk-adjusted returns helps traders to properly plan their investments and make wise financial decisions. Volatility can help traders extract good returns if they know how to adjust for the risks involved in volatile scenarios. You are more likely to get good returns.
You can also use the Python code provided above for each means of adjusting risk in your strategy.
To learn more about volatility and risk-adjusted returns, enroll in the following courses: volatility trading strategyIn this course you will learn four different ways of measuring volatility: ATR, standard deviation, VIX and beta. It helps you set dynamic stop-loss and take-profit levels, hedge your portfolio with the VIX, and select stocks in your portfolio.
Note: The original post was revised on January 18, 2023 for accuracy and currency.
Disclaimer: All investments and trading in the stock market involve risk. Any decision to trade in the financial markets, including trading in stocks, options, or other financial instruments, should be made only after thorough investigation, including personal risk and financial assessment, and the involvement of professional assistance. It’s a personal decision to be made. I think it is necessary. Any trading strategies or related information provided in this article are for informational purposes only.

